Accueil > Sondages > Comment réaliser une enquête > Taille d’un échantillon aléatoire et Marge d’erreur

Taille d’un échantillon aléatoire et Marge d’erreur

vendredi 20 avril 2012, par François Daniel Giezendanner

Notez cet article

Introduction

Lorsque l’on effectue une enquête on s’intéresse à une population mère (population totale) dont on va généralement interroger une petite partie, c’est l’échantillon dont il faut déterminer la taille soigneusement car elle a une grande importance sur la précision des estimations réalisées sur les caractéristiques de la population-mère.

Pour des raisons économiques, il est nécessaire d’utiliser une taille d’échantillon la plus réduite possible tout en obtenant un taux de confiance et une marge d’erreur suffisants.

Paramètres en jeux

Dans ce qui suit on appelle :

N : Taille de la population-mère (ou population parent, ou population de référence, ou population d’origine).
n : Taille de l’échantillon pour une population mère très grande (infinie).
n2 : Taille de l’échantillon pour une population mère limitée et un rapport du taux d’échantillon qui est supérieur à 1/7 de la population mère.
s : Seuil de confiance (ou Niveau de confiance ou encore Taux de confiance) que l’on souhaite garantir sur la mesure.
t : Coefficient de marge déduit du Taux de confiance « s ».
e : Marge d’erreur que l’on se donne pour la grandeur que l’on veut estimer (par exemple on veut connaître la proportion réelle à 5% près).
p : Proportion (connue ou supposée, estimée) des éléments de la population-mère qui présentent une propriété donnée. (lorsque p est inconnue, on utilise p = 0.5). (on dit ausi : Probabilité de succès ou probabilité de réalisation positive).
q = 1-p : Probabilité d’échec ou probabilité de réalisation négative.

On définit également :

Le Taux de sondage R = n/N
La Fourchette d’incertitude I = 2e.

La théorie statistique fourni les équations qui expriment les relations entre ces paramètres.

Les Taux de confiance « s » les plus utilisés et les Coefficients de marge « t » associés sont donnés dans le tableau suivant :

**Tableau 1**
Taux de confiance « s »	Coefficient de marge « t »	« t² »
80%	1.28	1.6384
85%	1.44	2.0736
90%	1.645	2.6896
95%	1.96	3.8416
96%	2.05	4.2025
98%	2.33	5.4280
99%	2.575	6.6049

1. POPULATION MERE INFINIE

Cas de l’échantillon indépendant (non exhaustif)

La formule donnant la taille « n » minimum de l’échantillon est la suivante :

$\mathbf{n=\frac{t^{2}p(1-p)}{e^{2}}}$

et sa réciproque

$\mathbf{e=t\sqrt{\frac{p(1-p)}{n}}}$

« n » étant proportionnel à l’inverse du carré de « e » cela signifie que pour diviser la marge d’erreur par 2 il faut multiplier la taille de l’échantillon « n » par 4.

Valeurs calculées de la Taille de l’échantillon « n »

Les deux tableaux ci-dessous présentent la taille n des échantillons pour 2 niveaux de confiance s = 95% et s = 99% et différentes proportion p de la population mère.

**Tableau 2 : TAILLE « n » DES ECHANTILLONS pour un Niveau de confiance s = 95%, donc t = 1.96**
Proportion « p »	« q=1-p »	Marge d’erreur « e »
		0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09	0.1
0.1	0.9	3’457	864	384	216	138	96	71	54	43	35
0.2	0.8	6’147	1’537	683	384	246	171	125	96	76	61
0.3	0.7	8’067	2’017	896	504	323	224	165	126	100	81
0.4	0.6	9’220	2’305	1’024	576	369	256	188	144	114	92
0.5	0.5	9’604	2’401	1’067	600	384	267	196	150	119	96

**Tableau 3 : TAILLE « n » DES ECHANTILLONS pour un Niveau de confiance s = 99%, donc t = 2.57**
Proportion « p »	« q=1-p »	Marge d’erreur « e »
		0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09	0.1
0.1	0.9	5’944	1’486	660	372	238	165	121	93	73	59
0.2	0.8	10’568	2’642	1’174	660	423	294	216	165	130	106
0.3	0.7	13’870	3’468	1’541	867	555	385	283	217	171	139
0.4	0.6	15’852	3’963	1’761	991	634	440	324	248	196	159
0.5	0.5	16’512	4’128	1’835	1’032	660	459	337	258	204	165

Valeurs calculées de la Marge d’erreur « e »

Les deux tableaux ci-dessous présentent la Marge d’erreur « e » en fonction de la Taille « n » des échantillons pour 2 niveaux de confiance s = 95% et s = 99% et différentes proportion p de la population mère.

**Tableau 4 : MARGE D’ERREUR « e » pour un Niveau de confiance s = 95%, donc t = 1.96**
Taille échantillon « n »	Proportion « p » de la population mère
	p = 0.1	p = 0.2	p = 0.3	p = 0.4	p = 0.5
100	0.059	0.078	0.090	0.096	0.098
200	0.042	0.055	0.064	0.068	0.069
300	0.034	0.045	0.052	0.055	0.057
400	0.029	0.039	0.045	0.048	0.049
500	0.026	0.035	0.040	0.043	0.044
600	0.024	0.032	0.037	0.039	0.040
700	0.022	0.030	0.034	0.036	0.037
800	0.021	0.028	0.032	0.034	0.035
900	0.020	0.026	0.030	0.032	0.033
1’000	0.019	0.025	0.028	0.030	0.031
1’200	0.017	0.023	0.026	0.028	0.028
1’600	0.015	0.020	0.022	0.024	0.025
2’000	0.013	0.018	0.020	0.021	0.022
3’000	0.011	0.014	0.016	0.018	0.018
4’000	0.009	0.012	0.014	0.015	0.015
5’000	0.008	0.011	0.013	0.014	0.014
7’500	0.007	0.009	0.010	0.011	0.011
10’000	0.006	0.008	0.009	0.010	0.010
12’000	0.005	0.007	0.008	0.009	0.009
14’000	0.005	0.007	0.008	0.008	0.008
16’000	0.005	0.006	0.007	0.008	0.008

**Tableau 5 : MARGE D’ERREUR « e » pour un Niveau de confiance s = 99%, donc t = 2.57**
Taille échantillon « n »	Proportion « p » de la population mère
	p = 0.1	p = 0.2	p = 0.3	p = 0.4	p = 0.5
100	0.077	0.103	0.118	0.126	0.129
200	0.055	0.073	0.083	0.089	0.091
300	0.045	0.059	0.068	0.073	0.074
400	0.039	0.051	0.059	0.063	0.064
500	0.034	0.046	0.053	0.056	0.057
600	0.031	0.042	0.048	0.051	0.052
700	0.029	0.039	0.045	0.048	0.049
800	0.027	0.036	0.042	0.045	0.045
900	0.026	0.034	0.039	0.042	0.043
1’000	0.024	0.033	0.037	0.040	0.041
1’200	0.022	0.030	0.034	0.036	0.037
1’600	0.019	0.026	0.029	0.031	0.032
2’000	0.017	0.023	0.026	0.028	0.029
3’000	0.014	0.019	0.022	0.023	0.023
4’000	0.012	0.016	0.019	0.020	0.020
5’000	0.011	0.015	0.017	0.018	0.018
7’500	0.009	0.012	0.014	0.015	0.015
10’000	0.008	0.010	0.012	0.013	0.013
12’000	0.007	0.009	0.011	0.011	0.012
14’000	0.007	0.009	0.010	0.011	0.011
16’000	0.006	0.008	0.009	0.010	0.010

La représentativité de l’échantillon

En bref, un échantillon est dit représentatif lorsqu’il possède les mêmes caractéristiques que la population que l’on souhaite étudier.

Pour mieux définir ce concept nous prenons la définition de forum.cultureco.com :

Constituer un échantillon représentatif c’est faire en sorte que les composantes essentielles de sa population de référence figurent dans l’échantillon, dans des proportions identiques.

A cette condition, les résultats observés sur l’échantillon peuvent être extrapolés à l’ensemble de sa population de référence.

Autrement dit, on qualifie de représentatif un échantillon, à partir du moment où il reflète le plus exactement possible sa population de référence, tant dans sa diversité que dans ses proportions.

Pour prélever un échantillon représentatif, on peut recourir à 2 familles de méthodes : les méthodes probabilistes et les méthodes empiriques.

Vous trouverez en fin d’article une liste de documents intéressants qui traitent ce sujet.

Fiabilité de l’échantillon

La relation ci-dessus montre que la taille n de l’échantillon dépend :

de t donc du Seuil de confiance s,
de la Proportion p des éléments de la population-mère et
de la Marge d’erreur e.

La fiabilité d’un échantillon est représentée par le seuil de confiance s et par la marge d’erreur e.

Considérons un échantillon du Tableau 2 ci-dessus, il est définis avec un seuil de confiance s de 95%, cela signifie 5% de risque de nous tromper (1 sur 20). Acceptons une marge d’erreur e de 2% et considérons que la Proportion p dans la population mère est de 40%, la taille de l’échantillon est alors de 2305. Donc en terme de fiabilité, cela signifie qu’avec cet échantillon on à 95% de chance (on a 5% de risque de se tromper) qu’un résultat qui vaut 40% est sûr à + ou - 2%, c’est à dire qu’il est compris entre 38% et 42%. En d’autres termes seuls 5% de l’échantillon sera en dehors de cet intervalle 38% - 42%.

Cette problématique de la Fiabilité de l’échantillon est très largement présentée sur le Web, on se reportera par exemple à l’article Comment réaliser une enquête par questionnaire ? de surveystore.info et plus généralement à la bibliographie :

Problématique de la fiabilité de l’échantillon

2. POPULATION MERE FINIE

Cas de l’échantillon exhaustif

cf. : Deuxième partie : la méthode d’étude

Lorsque le taux d’échantillon est supérieur à 1/7 de la population mère « N » (population totale), la taille « n » de l’échantillon déterminée précédemment doit être corrigée. La nouvelle taille « n2 » corrigée de l’échantillon est égale à :

$\mathbf{n2=n\frac{N-n}{N-1}}$

donc :

$\mathbf{n2=\frac{t^{2}p(1-p)}{e^{2}}*\frac{N-n}{N-1}}$

et « e » vaut alors (Cf. Annexe 5) :

$\mathbf{e=t\sqrt{\frac{p(1-p)}{n}}*\sqrt{\frac{N-n}{N-1}}}$

Une rapide analyse de ces équations et d’autres considérations montrent que la Taille « n » d’un échantillon est d’autant plus grande que :

la Marge d’erreur « e » désirée est faible ;
le Niveau (Taux) de confiance « s » et donc le Coefficient de marge « t » désiré est élevé ;
la Proportion « p » à estimer est près de 50% ;
la Taille « N » de la population est grande.

L’équation utilisée dans l’article « Un peu de technique : L’échantillonnage » (site « sondages-ce.fr »)

L’équipe sondages-ce.fr nous donne sa recette pour déterminer la taille d’un échantillon adéquat.

Ils travaillent selon l’hypothèse d’un partage des opinions à parts égales. Ils supposent que l’opinion des membres de la population se partage « moitié-moitié », cela nous donnera la taille d’échantillon maximale que nous prendrons donc (sans présumer ainsi de la répartition des réponses).

En d’autres termes on fixe à 0.5 la Proportion (estimée) p des éléments de la population-mère qui présentent une propriété donnée (c’est la valeur utilisée lorsqu’elle est inconnue) , donc p = 0.5

Ils proposent la formule du calcul de la taille de l’échantillon suivante :

$\mathbf{n=\frac{t^{2}N}{t^{2}+(2e)^{2}(N-1)}}$

Cette formule est valable pour le cas particulier p = 0.5. La formule générale pour tous p est données plus bas. La taille de l’échantillon étudié fluctue ainsi uniquement en fonction de la largeur de la fourchette d’incertitude I = 2e, donc en fonction de la Marge d’erreur « e ».

Pour un Niveau (ou Taux) de confiance s = 95% (niveau très souvent utilisé), donc t = 1.96 :

$n=\frac{1.96^{2}N}{1.96^{2}+(2e)^{2}(N-1)}$

Pour un Niveau (ou Taux) de confiance s = 98%, donc t = 2.33 :

$n=\frac{2.33^{2}N}{2.33^{2}+(2e)^{2}(N-1)}$

Les 2 tableaux ci-dessous présentent la Taille « n » des échantillons en fonction de la population mère « N » :

**Tableau 6 : TAILLE « n » DES ECHANTILLONS pour p = 0.5 et un Niveau de confiance s = 95%, donc t = 1.96**
Taille de la Population Mère « N »	Marge d’erreur « e »
	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09	0.1
100	99	96	92	86	80	73	66	60	54	49
200	196	185	169	150	132	115	99	86	75	65
300	291	267	234	200	169	141	119	100	85	73
400	384	343	291	240	196	160	132	109	92	78
500	475	414	341	273	217	174	141	116	96	81
1’000	906	706	516	375	278	211	164	131	106	88
2’000	1’655	1’091	696	462	322	235	179	140	112	92
3’000	2’286	1’334	787	500	341	245	184	143	114	93
4’000	2’824	1’501	843	522	351	250	187	145	115	94
5’000	3’288	1’622	880	536	357	253	189	146	116	94
7’500	4’212	1’819	934	556	365	258	191	147	117	95
10’000	4’899	1’936	964	566	370	260	192	148	117	95
25’000	6’939	2’191	1’023	586	378	264	194	149	118	96
50’000	8’057	2’291	1’045	593	381	265	195	150	118	96
100’000	8’763	2’345	1’056	597	383	266	196	150	118	96
1’000’000	9’513	2’395	1’066	600	384	267	196	150	119	96
2’500’000	9’567	2’399	1’067	600	384	267	196	150	119	96
4’000’000	9’581	2’400	1’067	600	384	267	196	150	119	96
10’000’000	9’595	2’400	1’067	600	384	267	196	150	119	96
50’000’000	9’602	2’401	1’067	600	384	267	196	150	119	96

**Tableau 7 : TAILLE « n » DES ECHANTILLONS pour p = 0.5 et un Niveau de confiance s = 99%, donc t = 2.57**
Taille de la Population Mère « N »	Marge d’erreur « e »
	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09	0.1
100	99	98	95	91	87	82	77	72	67	63
200	198	191	180	168	154	139	126	113	101	91
300	295	280	258	233	207	182	159	139	122	107
400	391	365	329	288	249	214	183	157	135	117
500	485	446	393	337	285	239	202	170	145	124
1’000	943	805	647	508	398	315	252	205	169	142
2’000	1’784	1’347	957	681	497	373	289	229	185	153
3’000	2’539	1’738	1’139	768	541	398	303	238	191	157
4’000	3’220	2’032	1’258	821	567	412	311	242	194	159
5’000	3’838	2’261	1’342	856	584	420	316	245	196	160
7’500	5’158	2’663	1’474	907	607	432	323	249	198	162
10’000	6’228	2’922	1’550	936	620	439	326	252	200	162
25’000	9’944	3’543	1’709	991	644	450	333	255	202	164
50’000	12’413	3’813	1’770	1’011	652	455	335	257	203	165
100’000	14’172	3’964	1’802	1’021	656	457	336	257	203	165
1’000’000	16’244	4’111	1’831	1’031	660	458	337	258	204	165
2’500’000	16’404	4’121	1’833	1’032	660	459	337	258	204	165
4’000’000	16’444	4’124	1’834	1’032	660	459	337	258	204	165
10’000’000	16’485	4’126	1’834	1’032	660	459	337	258	204	165
50’000’000	16’507	4’128	1’835	1’032	660	459	337	258	204	165

Les 6 tableaux ci-dessus sont calculés dans le tableur Open-Office. Le fichier est :


Calcul de la Taille des échantillons

L’équation ci-dessus utilisée par l’équipe « sondages-ce.fr » est un cas particulier pour p=0. 5 de l’équation démontrée dans les documents de Yves Aragon, Camelia Goga et Anne Ruiz-Gazen, M2 Statistique & Econométrie - Cours de sondage - Chapitre 1 à 5 (page 20), Théorie des sondages : cours 1 (page 43) et Initiation `a la théorie des sondages : cours IREM-Dijon (page 27). En effet, on y trouve la démonstration de la relation :

$\mathbf{n\geq \frac{t^{2}*\frac{N}{N-1}*p*(1-p)}{e^{2}+t^{2}*\frac{p*(1-p)}{N-1}}}$

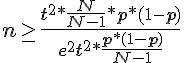
que l’on peut réarranger comme suit :

$\mathbf{n\geq \frac{\frac{N}{N-1}*p*(1-p)}{\frac{e^{2}}{t^{2}}+\frac{p*(1-p)}{N-1}}}$

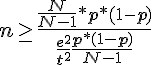
soit

$\mathbf{n\geq \frac{N*p*(1-p)}{\frac{e^{2}}{t^{2}}*(N-1)+p*(1-p)}}$

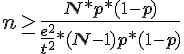
ou comme suit :

$\mathbf{n\geq \frac{t^{2}*N*p*(1-p)}{e^{2}*(N-1)+t^{2}*p*(1-p)}}$

soit :

$\mathbf{n\geq \frac{t^{2}*N}{\frac{e^{2}}{p*(1-p)}*(N-1)+t^{2}}}$

Dans le cas particulier où p = 0.5, on obtient :

$\mathbf{n\geq \frac{t^{2}*N}{\frac{e^{2}}{0.5^{2}}*(N-1)+t^{2}}}$

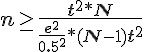
et on retrouve ainsi l’équation utilisée par l’équipe « sondage-ce.fr » puisque 1/(0.5*0.5) = 2*2 :

$\mathbf{n\geq \frac{t^{2}*N}{(2e)^{2}*(N-1)+t^{2}}}$

Marge d’erreur e :

A l’annexe 5 on montre que depuis l’équation ci-dessus on obtient :

$\mathbf{e\geq t*\sqrt{\frac{p*(1-p)*(N-n)}{n*(N-1)}}}$

Sources :

M2 Statistique & Econométrie - Cours de sondage - Chapitre 1 à 5
Yves Aragon, Camelia Goga et Anne Ruiz-Gazen, 14 octobre 2009
A la page 20
http://www-gremaq.univ-tlse1.fr/stat/Anneweb/chap1a5.pdf

Théorie des sondages : cours 1
Camelia Goga. IMB, Université de Bourgogne
A la page 43
http://math.u-bourgogne.fr/IMB/goga/cours1_sondage_Besancon.pdf

Initiation `a la théorie des sondages : cours IREM-Dijon
Camelia Goga. IMB, Université de Bourgogne. Dijon, 12 novembre 2009
A la page 27
http://math.u-bourgogne.fr/IMB/goga/expose_irem_2009.pdf

D’autres corrections approchantes sont proposées dans la littérature, nous les présentons en annexe.

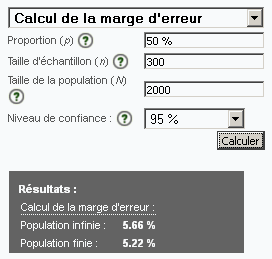
Illustrations des Marges d’erreur « e », des proportion des éléments « p », des Tailles de la population mère « N » et des échantillons « n »

Les calculateurs en ligne :

Calculateur en ligne de RMPD
http://www.rmpd.ca/calculators.php

Calculateur en ligne de CubeRecherche
http://www.cuberecherche.ca/frcalculateurs.php

ou d’autres calculateurs en ligne mentionnés vous donnerons des résultats similaires à ceux des tableau ci-dessous de TAKTO calculés pour un Niveau de confiance s de 95%.

n = Taille Echantillon , p = 50%
N = Taille Population mère	e = Marge d’erreur
N = Taille Population mère	0,01	0,025	0,05	0,1
100	100	95	81	51
1’000	910	616	287	92
10’000	5’001	1’381	386	101
100’000	9’092	1’576	400	101
infinie	10’001	1’601	401	101

n = Taille Echantillon , p = 40% ou p = 60%
N = Taille Population mère	e = Marge d’erreur
N = Taille Population mère	0,01	0,025	0,05	0,1
100	99	94	80	50
1’000	906	607	279	89
10’000	4’899	1’333	371	97
100’000	8’761	1’514	384	97
infinie	9’601	1’537	385	97

n = Taille Echantillon , p = 30% ou p = 70%
N = Taille Population mère	e = Marge d’erreur
N = Taille Population mère	0,01	0,025	0,05	0,1
100	99	94	78	47
1’000	894	574	253	79
10’000	4’566	1’186	327	85
100’000	7’750	1’328	336	85
infinie	8’401	1’345	337	85

n = Taille Echantillon , p = 20% ou p = 80%
N = Taille Population mère	e = Marge d’erreur
N = Taille Population mère	0,01	0,025	0,05	0,1
100	99	92	73	40
1’000	865	507	205	62
10’000	3’904	930	251	65
100’000	6’016	1’015	257	65
infinie	6’401	1’025	257	65

n = Taille Echantillon , p = 10% ou p = 90%
N = Taille Population mère	e = Marge d’erreur
N = Taille Population mère	0,01	0,025	0,05	0,1
100	98	86	60	28
1’000	783	367	127	36
10’000	2’648	546	143	37
100’000	3’476	574	145	37
infinie	3’601	577	145	37

TAILLE D’ÉCHANTILLON ET MARGE D’ERREUR
http://www.takto.qc.ca/infotakto/it0402.pdf

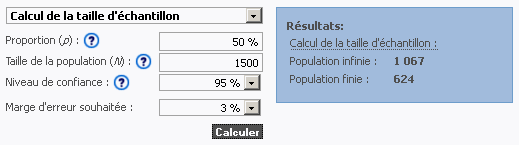
Précision et Taille

Pour un niveau de confiance de 0.95, l’échantillon à retenir s’établit à :

Calculateur RMPD

+ source complémentaire : Détermination de la taille d’un échantillon aléatoire

Conditions générales

Proportion « p » : 50%
Niveau de confiance « s » : 95%
Marge d’erreur « e » souhaitée :
Taille de l’échantillon pour une Population infinie, « n » :
Taille de l’échantillon pour une Population finie, « n2 » :

Cas 1 : Taille de la Population mère « N » : 1’000’000

Marge d’erreur « e »	« n2 » (Taille échantillon pour Population mère N finie N = 1’000’000)	« n » (Taille échantillon pour Population mère N infinie)
0.01	9’513	9’604
0.02		2’401
0.03	1’066	1’067
0.04	600
0.05	384	384
0.06	267
0.10	96	96

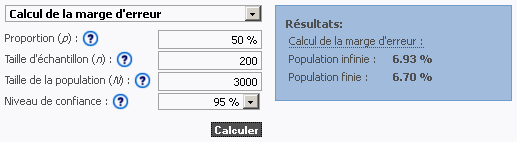
Cas 2 : Taille de la Population mère (N) : 10’000

Marge d’erreur « e »	« n2 » (Taille échantillon pour Population mère N finie N = 10’000)	« n » (Taille échantillon pour Population mère N infinie)
0.01	4’899	9’604
0.03	964	1’067
0.05	370	384
0.10	95	96

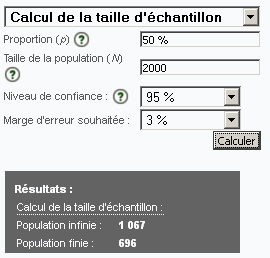
Cas 3 : Taille de la Population mère (N) : 1’000

Marge d’erreur « e »	« n2 » (Taille échantillon pour Population mère N finie N = 1’000)	« n » (Taille échantillon pour Population mère N infinie)
0.01	906	9’604
0.03	516	1’067
0.05	278	384
0.10	88	96

Cas 4 : Taille de la Population mère (N) : 100

Marge d’erreur « e »	« n2 » (Taille échantillon pour Population mère N finie N = 100)	« n » (Taille échantillon pour Population mère N infinie)
0.01	99	9’604
0.03	92	1’067
0.05	80	384
0.10	49	96

3. BIAIS D’ÉCHANTILLONNAGE - PLAN D’ÉCHANTILLONNAGE

Nous donnons ici trois exemples de calculs d’échantillons dans des situations différentes.

Exemple 1 : Comment calculer l’échantillon de départ et le rendement du plan échantillonnal

Ainsi qu’expliqué par Claire Durand :

l’échantillon de départ nécessaire se calcule en prenant l’échantillon théorique (c’est-à-dire la taille d’échantillon que l’on vise à obtenir lorsque l’enquête sera terminée) que l’on multiplie par l’inverse des taux de validité, d’éligibilité – et d’incidence lorsque pertinent – et de réponse estimés :

Dans ses documents de cours Cours Méthodes de sondage,
Notes de cours - L’échantillon, combien d’unités doit-on prendre ? et Méthodes de sondage - SOL3017 - Notes de cours, deuxième partie, Claire Durand explique de manière détaillée comment tenir compte du Biais de la base de sondage :

Pour compenser le biais il faut tenir compte de :

la qualité de la liste (la validité des unités sélectionnées)
la qualité des unités inscrites sur la liste (l’éligibilité des unités sélectionnées et l’incidence)
du taux de réponse

Cela conduit à définir quatre taux :

Taux de réponse = tx-reponse
Taux d’éligibilité = tx-eligib
Taux d’incidence = tx-incidence
Taux de validité = tx-validite

et à appliquer la formule :

$\mathbf{n_{depart}=n_{theorique}*\frac{1}{tx-reponse}*\frac{1}{(tx-eligib)*(tx-incidence)}*\frac{1}{tx-validite}}$

Exemple d’application :

Le taux de réponse prévu est de 60% (0,6)
Le taux d’éligibilité estimé est de 95% (0,95)
Et le taux de validité de la liste est de 80% (0,8) et le taux d’incidence = 1
Et que je désire avoir 384 personnes dans l’échantillon (marge d’erreur de 5%)

il faut faire le calcul suivant :

$\mathbf{n_{depart}=384*\frac{1}{0.6}*\frac{1}{0.95}*\frac{1}{0.8}=842}$

Il faut donc sélectionner 842 unités pour espérer obtenir 384 répondants dans ces conditions.

Sources :

Cours Méthodes de sondage
© Claire Durand, Département de sociologie, Université de Montréal
L’échantillon, combien ? Échantillon théorique, échantillon de départ, pas, pondération
https://www.webdepot.umontreal.ca/Enseignement/SOCIO/Intranet/Sondage/public/presentations/echantillon_combienshwdoc.pdf

Notes de cours - L’échantillon, combien d’unités doit-on prendre ?
Département de sociologie - Université de Montréal - Professeur : Claire Durand - © Claire Durand 2009
https://www.webdepot.umontreal.ca/Enseignement/SOCIO/Intranet/Sondage/public/notesdecours/echantillon_combien.pdf

Méthodes de sondage - SOL3017 - Notes de cours, deuxième partie
L’échantillonnage - La gestion du terrain
Département de sociologie, Université de Montréal, professeur : Claire Durand 2002
http://www.mapageweb.umontreal.ca/durandc/Enseignement/MethodesDeSondage/echantillon.pdf

Exemple 2 : Effet du plan d’échantillonnage (enquête par grappe)

Dans cet article de ifad.org ils procèdent comme suit :

Deuxième étape : Effet du plan d’échantillonnage

L’enquête anthropométrique repose sur un échantillon en grappes (sélection représentative de villages), et non pas sur un échantillon aléatoire simple. Pour corriger la différence, on multiplie la taille de l’échantillon par l’effet du plan d’échantillonnage (D).

On suppose généralement que cet effet est de 2 pour les enquêtes nutritionnelles faisant appel au sondage en grappes.

Exemple

n x D = 323 x 2 = 646

Troisième étape : Impondérables

On ajoute encore 5% à l’échantillon pour tenir compte d’impondérables comme les non-réponses ou les erreurs d’enregistrement.

Exemple

n + 5% = 646 x 1.05 = 678.3 ˜ 678

Quatrième étape : Distribution des sujets observés

Pour conclure, on arrondit le chiffre obtenu au nombre le plus proche du nombre de grappes (30 villages) à étudier.

Trente est le nombre type de grappes fixé par le Programme élargi de vaccination de l’OMS (enquêtes en grappes du PEV). Il n’y a pas de raison statistique logique de s’en tenir exactement à 30 grappes et le nombre peut être ajusté en cas de nécessité impérieuse.

Exemple

Taille d’échantillon finale : N = 690 enfants

On divise ensuite la taille d’échantillon finale (N) par le nombre de grappes (30) pour déterminer le nombre de sujets à observer par grappe.

Exemple

N ÷ no. grappes = 690 ÷ 30 = 23 enfants par village

Donc ici, l’Effet du plan d’échantillonnage a pour résultat de faire passer l’échantillon de 323 à 690.

Source :

Calcul de la taille de l’échantillon - Calculating the Sample Size
Deuxième étape : Effet du plan d’échantillonnage
http://www.ifad.org/gender/tools/hfs/anthropometry/f/ant_3.htm
http://www.ifad.org/gender/tools/hfs/anthropometry/ant_3.htm

Exemple 3 : Déterminer la taille de l’échantillon pour une enquête par grappe à indicateurs multiples

Dans CHAPITRE 4 - CONCEPTION ET TIRAGE DE L’ÉCHANTILLON on explique comment déterminer la taille de l’échantillon pour une enquête par grappe à indicateurs multiples.

La taille de l’échantillon est peut-être le paramètre le plus important du plan de sondage car elle affecte la précision, le coût et la durée de l’enquête plus que tout autre facteur.

CALCUL DE LA TAILLE DE L’ECHANTILLON

Le calcul de la taille de l’échantillon à l’aide de formules mathématiques appropriées nécessite que certains facteurs soient spécifiés et, que pour d’autres, vous posiez des hypothèses ou que vous utilisiez des valeurs tirées d’enquêtes précédentes ou similaires. Ces facteurs sont les suivants :

La précision ou la marge d’erreur relative recherchée ;
Le niveau de confiance souhaité ;
La proportion de la population estimée (ou connue) dans un groupe cible donné ;
Le taux de couverture - ou la prévalence - prévu ou anticipé d’un indicateur donné ;
L’effet du plan de sondage (deff) ;
La taille moyenne du ménage ;
Un coefficient d’ajustement pour les cas éventuels de non-réponses.

Le calcul de la taille de l’échantillon s’applique seulement aux personnes, même si elle est exprimée en termes de nombre de ménages que vous devriez visiter pour interviewer des individus.

La formule de calcul est donnée ci-dessous :

$\mathbf{n=\frac{4*r*(1-r)*f*1.1}{(0.1*2*r)^{2}*p*nh}}$

Où :

n est la taille requise de l’échantillon - exprimée en nombre de ménages - pour
l’indicateur-CLÉ (voir la section qui suit pour la détermination de cet indicateur clé)
4 est un facteur pour atteindre 95% d’intervalle de confiance
r est la prévalence (taux de couverture) prévue ou anticipée pour l’indicateur-clé à
estimer
1,1 est le facteur nécessaire pour augmenter la taille de l’échantillon de 10% afin de
tenir compte du taux de non réponse
f est le symbole représentant l’effet du plan de sondage - deff
0,12r est la marge d’erreur raisonnable pour un intervalle de confiance de 95%,
définie comme 12 pour cent de r (12% est donc la marge d’erreur relative de r)
p est la proportion de la population totale sur laquelle l’indicateur, r, est basé, et
nh est la taille moyenne du ménage.

Source :

CHAPITRE 4 - CONCEPTION ET TIRAGE DE L’ÉCHANTILLON
MANUEL DE L’ENQUETE PAR GRAPPES A INDICATEURS MULTIPLES
Ce chapitre technique1 s’adresse principalement aux spécialistes de sondage, mais aussi
au coordinateur et aux autres responsables techniques de l’enquête.
http://www.childinfo.org/files/Chapitre_4_-_Conception_et_tirage_de_lechantillon_060219.pdf

4. ANNEXES : Lorsque N n’est pas très grand

Annexe 1

Lorsque N n’est pas très grand, il convient d’ajuster la taille estimée par l’équation :

$\mathbf{n2=\frac{n}{1+\frac{n+1}{N}}\approx \frac{n}{1+\frac{n}{N}}}$

$\mathbf{n2=\frac{n}{1+\frac{n+1}{N}}=\frac{n*N}{N+n+1}}$

$\mathbf{n2 \approx \frac{n}{1+\frac{n}{N}}=\frac{n*N}{n+N}}$

Le choix de l’échantillon
http://perso.univ-rennes1.fr/benoit.le-maux/Echantillon.pdf

DOCUMENT 2.1 : INFORMATIONS COMPLEMENTAIRES SUR LA METHODE
D’ENQUETE
http://www.optigede.ademe.fr/sites/default/files/u153/Document2_1_methode_enquete.pdf

Chapitre 3 - Détermination de la taille de l’échantillon
http://www.alalouf.com/4280/Chapitres/%C9chantillonnageChap3.pdf

Annexe 2

$\mathbf{n2=\frac{n*N}{n+N}}$

Les études quantitatives
http://aesplus.net/Les-etudes-quantitatives.html

Annexe 3

$\mathbf{n2=\frac{n}{\frac{n+(N-1)}{N}}=\frac{n*N}{n+N-1}}$

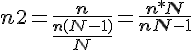
variable normale centrée réduite
les distribution d’échantillonnage
http://www.google.ch/url?sa=t&rct=j&q=%22variable%20normale%20centr%C3%A9e%20r%C3%A9duite%22%20%22une%20variable%20centr%C3%A9e%20r%C3%A9duite%20est%20une%20variable%22&source=web&cd=2&ved=0CC8QFjAB&url=http%3A%2F%2Fwww.er.uqam.ca%2Fnobel%2Fr26360%2Feut%2Fcour11tr%2Fdiechant.ppt&ei=TY6VT_OYDYOeOq7QuPYD&usg=AFQjCNFbQ228rBgp-HhYsQ9_oFI_8UvDqA&cad=rja

Annexe 4

$\mathbf{n2=\frac{p*(1-P)+\frac{e^{2}}{t^{2}}}{\frac{p*(1-P)}{N}+\frac{e^{2}}{t^{2}}}=\frac{\frac{t^{2}p(1-p)}{e^{2}}+1}{\frac{\frac{t^{2}p(1-p)}{e^{2}}}{N}+1}}$

$\mathbf{n2=\frac{n+1}{\frac{n}{N}+1} = \frac{(n+1)*N}{n+N}}$

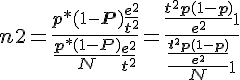
Méthodes de sondage - SOL3017 - Notes de cours, deuxième partie
L’échantillonnage - La gestion du terrain
Département de sociologie, Université de Montréal, professeur : Claire Durand 2002
http://www.mapageweb.umontreal.ca/durandc/Enseignement/MethodesDeSondage/echantillon.pdf

Méthodes et pratiques d’enquête
A la page 173
Statistique Canada, 2010, 434 pages
http://www.statcan.gc.ca/pub/12-587-x/12-587-x2003001-fra.pdf
http://www5.statcan.gc.ca/bsolc/olc-cel/olc-cel?catno=12-587-x&lang=fra

Annexe 5 : Marge d’erreur pour l’échantillon exhaustif

On part de la formule générale :

$\mathbf{n\geq \frac{t^{2}*N}{\frac{e^{2}}{p*(1-p)}*(N-1)+t^{2}}}$

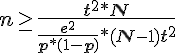
et on réarange comme suit :

$\mathbf{\frac{e^{2}}{p*(1-p)}*(N-1)+t^{2}\geq \frac{t^{2}*N}{n}}$

$\mathbf{\frac{e^{2}}{p*(1-p)}*(N-1)\geq \frac{t^{2}*(N-n)}{n}}$

$\mathbf{e^{2}\geq \frac{t^{2}*p*(1-p)*(N-n)}{n*(N-1)}}$